兰顿蚂蚁(Langton’s Ant)
兰顿蚂蚁是细胞自动机的例子。它由克里斯托夫·兰顿在1986年提出,它由黑白格子和一只”蚂蚁”构成,是一个二维图灵机。兰顿蚂蚁拥有非常简单的逻辑和复杂的表现。在2000年兰顿蚂蚁的图灵完备性被证明。兰顿蚂蚁的想法后来被推广,比如使用多种颜色。
游戏规则
在平面上的正方形格被填上黑色或白色。在其中一格正方形有一只「蚂蚁」。它的头部朝向上下左右其中一方。
- 若蚂蚁在白格,右转90度,将该格改为黑格,向前移一步;
- 若蚂蚁在黑格,左转90度,将该格改为白格,向前移一步。

行为模式
若从全白的背景开始,在一开始的数百步,蚂蚁留下的路线会出现许多对称或重复的形状,然后会出现类似混沌的假随机,至约一万步后会出现以104步为周期无限重复的「高速公路」朝固定方向移动。在目前试过的所有起始状态,蚂蚁的路线最终都会变成高速公路,但尚无法证明这是无论任何起始状态都会导致的必然结果。
沿伸
除了两种颜色分别让蚂蚁左转或右转,也可以定义更多种颜色进行循环。通用的表示方法是用 L 和 R 依序表示各颜色是左转还是右转,兰顿蚂蚁的规则即可表示为 RL。有些规则会产生对称或重复的形状。另外除了用方格,也可以用其他如六角形的格子。
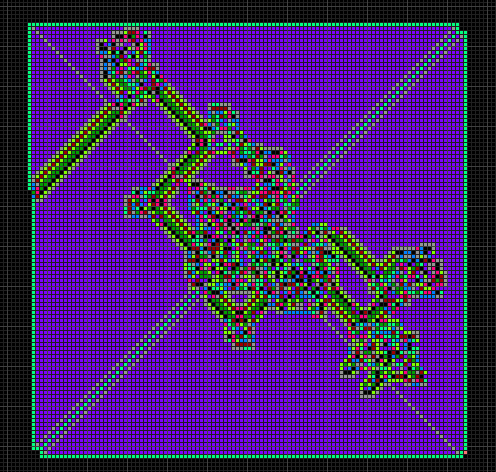
| 一些使用多种颜色的兰顿蚂蚁的示例 | |||
| RLR:混沌的生长,没有证实会产生高速公路 | LLRR:对称的生长 | LRRRRRLLR:形成方块 | LLRRRLRLRLLR:生成高速公路 |
 |
 |
 |
 |
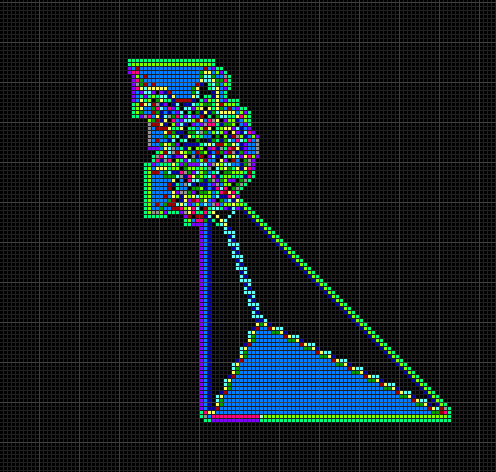
| RRLLLRLLLRRR:生成一个移动并生长的实心三角形 | L2NNL1L2L1:六边形循环生长 | L1L2NUL2L1R2:六边形螺旋生长 | R1R2NUR2R1L2:动画 |
 |
 |
 |
 |
Python 代码
import os
import random
import time
periods = 11000
m = 60
n = 102
cells = [[0] * n for i in range(m)]
# 0 -x, 1 +y, 2 +x, 3 -y
direct = random.randint(0, 3)
cells = [[0] * n for i in range(m)]
i = random.randint(0, m - 1)
j = random.randint(0, n - 1)
cells[i][j] = 1
for k in range(periods):
os.system('clear')
print "Step %d" % (k + 1)
if cells[i][j] == 1:
direct = (direct - 1) % 4
cells[i][j] = 0
else:
direct = (direct + 1) % 4
cells[i][j] = 1
if direct == 0:
j = (j - 1) % n
elif direct == 1:
i = (i - 1) % m
elif direct == 2:
j = (j + 1) % n
else:
i = (i + 1) % m
for x in range(m):
for y in range(n):
if cells[x][y] == 1:
print '*',
else:
print ' ',
print
time.sleep(0.05)