利用 SciPy 实现层次聚类

层次聚类算法的主要优点在于我们无需事先知道最终所需集群数量。很遗憾的是，网上并没有很详细的教程讲述如何使用 SciPy 的层次聚类包进行层次聚类。本教程将帮助你学习如何使用 SciPy 的层次聚类模块。

命名规则

在我们开始之前，我们先设定一下命名规则来帮助理解本篇教程：

X - 实验样本（n 乘 m 的数组）
n - 样本数量
m - 样本特征数量
Z - 集群关系数组（包含层次聚类信息）
k - 集群数量

导入所需模块及环境搭配

from matplotlib import pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage
import numpy as np

%matplotlib inline
np.set_printoptions(precision=5, suppress=True)

生成实验样本

如果你已经有自己的实验样本了，那么你可以选择跳过此步骤。但是要注意的是，你必须确保你的实验样本是一个 NumPy 矩阵 X，包含 n 个实验样本以及 m 个样本特征，即 X.shape == (n, m)。

# 生成两个集群: 集群 a 有100个数据点, 集群 b 有50个数据点:
np.random.seed(1029)
a = np.random.multivariate_normal([10, 0], [[3, 1], [1, 4]], size=[100,])
b = np.random.multivariate_normal([0, 20], [[3, 1], [1, 4]], size=[50,])
X = np.concatenate((a, b),)
plt.figure(figsize=(25, 10))
plt.scatter(X[:, 0], X[:, 1])
plt.show()

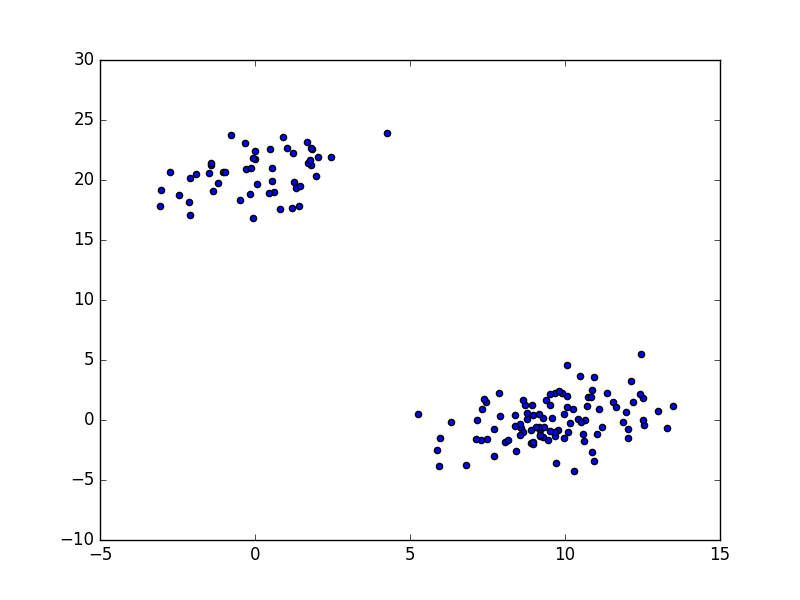
进行层次聚类

我们现在已经有了非常简单的实验样本，那我们来进行真正的聚类算法吧：

# 建立集群关系数组
Z = linkage(X, 'ward')

聚类结束。很简单吧 :smile:。不用惊讶，毕竟这是 Python 嘛。

在这一行代码中，根据 SciPy 的 linkage 模块文档所述，'ward' 是一种用于计算集群之间距离的方法。'ward' 表明 linkage() 方法会使用离差平方和算法。

使用 'ward' 是一个不错的选择。当然还有其他通用的距离算法，例如 'single'，'complete'，'average'。如果你了解这些算法，那么你可以选择使用这些方法进行层次聚类。

你可以使用 cophenet() 计算同表象相关系数来判断集群的性能。这个方程非常简单的比对了所有实验样本之间的距离和聚类之后的样本距离。如果这个值越接近于1，集群结果就更加完整的保存了实验样本间的实际距离。在我们的实验中，这个值非常接近于1：

from scipy.cluster.hierarchy import cophenet
from scipy.spatial.distance import pdist

c, coph_dists = cophenet(Z, pdist(X))
print c

0.9840295755

不管你使用了何种 method 和 metric，linkage() 方程都会利用这些方法计算集群间的距离，并在每一步合并距离最短的两个集群。linkage() 方程会返回一个长度为 n - 1 的数组，包含在每一步合并集群的信息：

print Z[0]

[ 124.       141.         0.07372    2.     ]

这个矩阵的每一行的格式是这样的 [idx, idx2, dist, sample_count]。

在第一步中，linkage 算法决定合并集群124和集群141，因为他们之间的距离为0.07372，为当前最短距离。这里的124和141分别代表在原始样本中的数组下标。在这一步中，一个具有两个实验样本的集群诞生了。

print Z[1]

[ 131.       139.         0.0753     2.     ]

在第二步中，linkage 算法决定合并集群131和集群139，因为他们之间的距离为0.0753，为当前最短距离。在这一步中，另一个具有两个实验样本的集群诞生了。

直到这一步，集群的下标和原本实验样本的下标是互相对应的，但是记住，我们只有150个实验样本，所以我们一共只有下标0至149。让我们来看看前20步：

print Z[:20]

[[ 124.       141.         0.07372    2.     ]
 [ 131.       139.         0.0753     2.     ]
 [ 136.       142.         0.07767    2.     ]
 [  10.        18.         0.08463    2.     ]
 [  60.        90.         0.09049    2.     ]
 [  30.        44.         0.1052     2.     ]
 [   4.        17.         0.1214     2.     ]
 [  56.       153.         0.15189    3.     ]
 [  58.        63.         0.16933    2.     ]
 [   2.        92.         0.17203    2.     ]
 [ 118.       119.         0.18263    2.     ]
 [  26.        99.         0.19047    2.     ]
 [  39.        64.         0.19385    2.     ]
 [ 117.       148.         0.20185    2.     ]
 [  50.        84.         0.20299    2.     ]
 [  55.        89.         0.2113     2.     ]
 [   3.        98.         0.2115     2.     ]
 [ 134.       144.         0.21395    2.     ]
 [ 120.       123.         0.21464    2.     ]
 [  23.       156.         0.21636    3.     ]]

直到前7步，此算法都在直接合并原有实验样本数据，也不难看出每一步的最短距离都在单调递增。在第8步中，此算法决定合并集群56和集群153。是不是很奇怪，我们只有150个数据点，何来的下标153？此算法中，任何 idx >= len(X) 的下标都指向在 Z[idx - len(X)] 中建立的集群。所以，第8步中，样本62与在第四步 Z[153 - 150] 中合并的集群（样本10和样本18）进行了合并。

让我们来看看这些数据点的坐标是不是反应了这一情况：

print X[[10, 18, 56]]

[[ 8.91446 -1.95095]
 [ 8.95663 -2.02432]
 [ 8.96876 -1.86035]]

看上去很接近，但是让我们再画图看看是不是这样：

idxs = [10, 18, 56]
plt.figure(figsize=(10, 8))
plt.scatter(X[:, 0], X[:, 1])
plt.scatter(X[idxs, 0], X[idxs, 1], c='r')
plt.show()

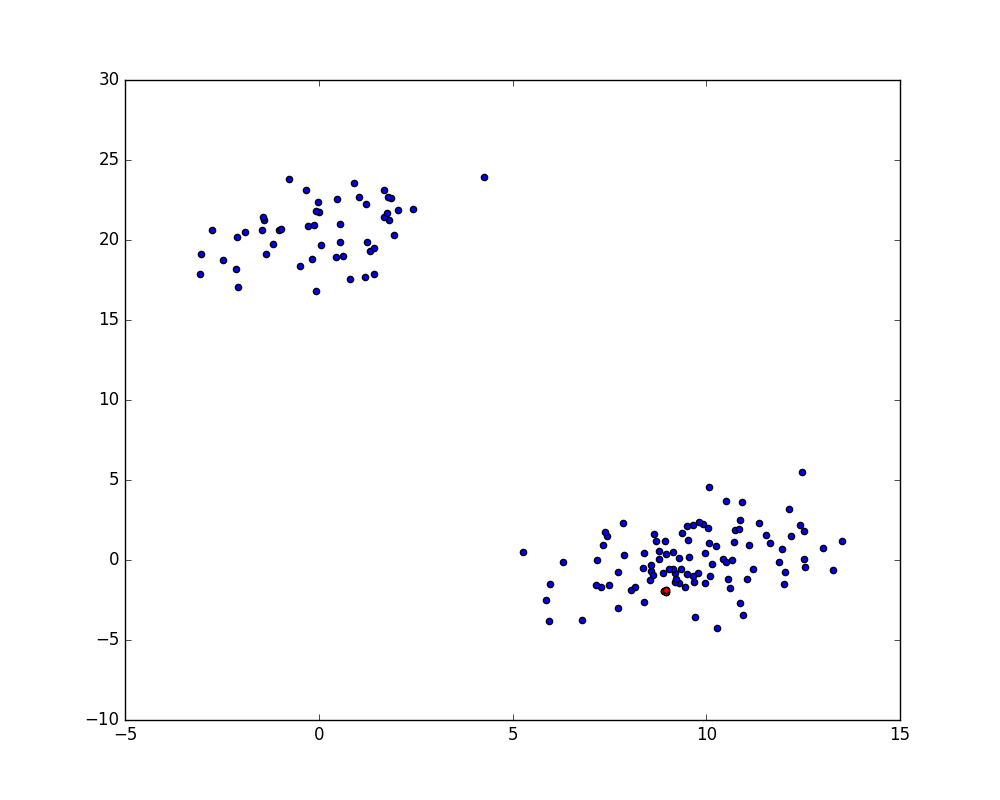
不难看出，这三个红点非常的接近，很好。

接下来我们先来看看这次层次聚类的树状图结果。

建立树状图

树状图展现了层次聚类中集群合并的顺序以及合并时集群间的距离。

plt.figure(figsize=(50, 10))
plt.title('Hierarchical Clustering Dendrogram')
plt.xlabel('sample index')
plt.ylabel('distance')
dendrogram(Z, leaf_rotation=90., leaf_font_size=8.
)
plt.show()

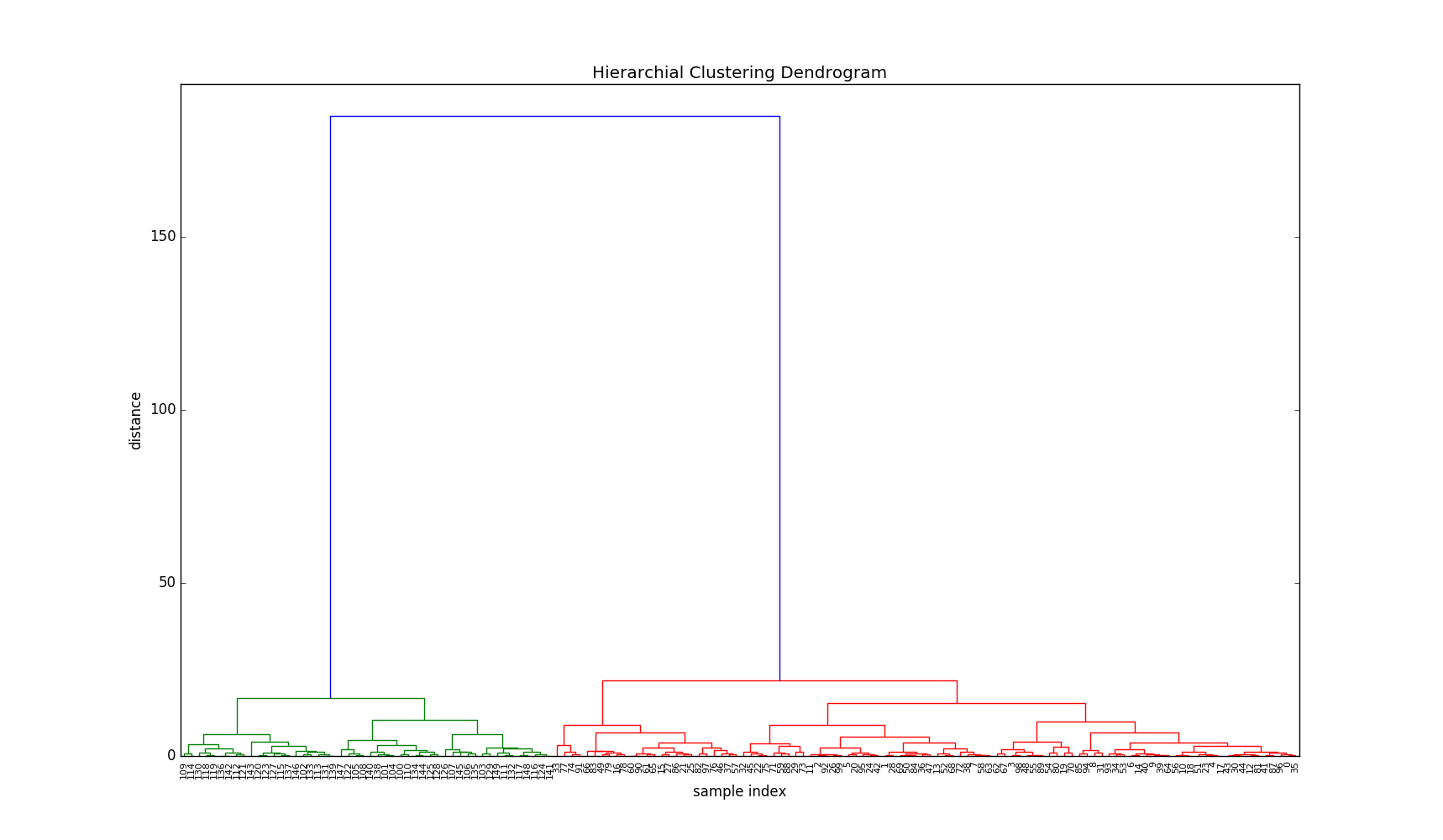
在树状图中，x 轴上的标记代表数据点在原有实验样本 X 中的下标，y 轴上表明集群间的距离。图像中，横线所在高度表明集群合并时的距离。

我们可以看到在 y 轴20处我们只有两个集群，但在最后的合并后，集群间的距离直线上升至180左右。让我们看看最后4步的集群间距离：

print Z[-4:, 2]

[  15.2525    16.79548   21.75623  185.07009]

这样的大距离跨度表明了在这一步中虽然有两个集群被合并了，但是它们可能不应该被合并。换句话说，它们可能本来就不属于同一个集群，它们就应该属于两个不同的集群。

在树状图中，我们可以看到绿色集群只包含了大于等于100的下标，而红色集群只包含了小于100的下标。看来我们的算法成功找出了实验样本中的两个集群。

缩减树状图

上一步得到的树状图非常大，然而它却仅仅包含了150个数据点。现实情况中，数据点可能更多。让我们来看看 dendrogram() 方程的其他参数：

plt.title('Hierarchical Clustering Dendrogram (truncated)')
plt.xlabel('sample index')
plt.ylabel('distance')
dendrogram(Z, truncate_mode='lastp', p=12, show_leaf_counts=False, leaf_rotation=90., leaf_font_size=12., show_contracted=True)
plt.show()

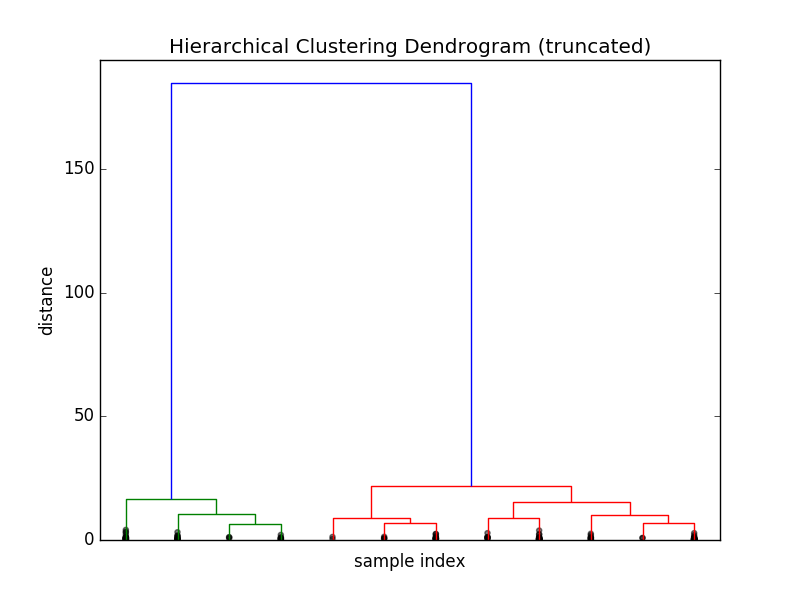
这幅树状图只包含了一共149次中的最后 p=12 次合并。你可能会发现 x 轴上的标签消失了，这是因为这些数据点已经被合并了。如果我们想更加直观的获得集群信息，我们可以通过以下代码：

plt.title('Hierarchical Clustering Dendrogram (truncated)')
plt.xlabel('sample index or (cluster size)')
plt.ylabel('distance')
dendrogram(Z, truncate_mode='lastp', p=12, leaf_rotation=90., leaf_font_size=12., show_contracted=True)
plt.show()

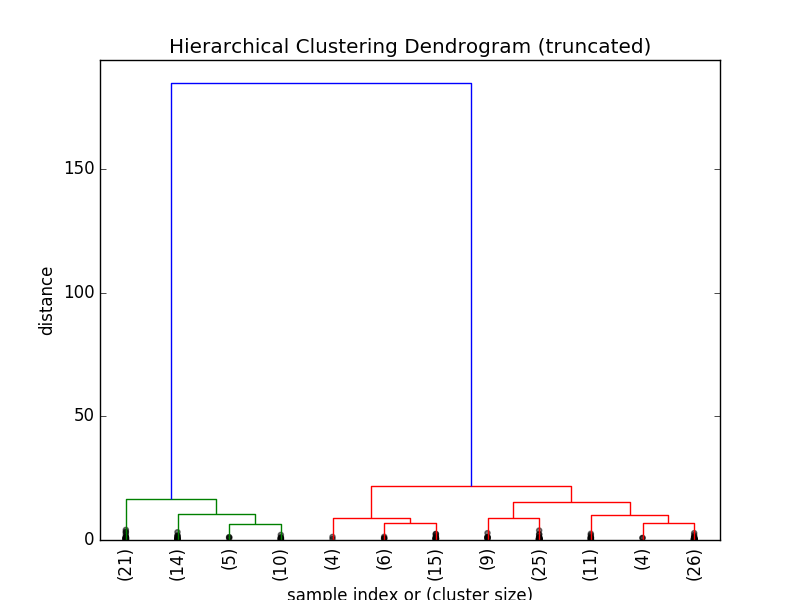
我们现在可以看到集群在最后12次合并中所包含的数据点数量。

更加好看的树状图

我们可以在树状图中显示集群间距离让树状图变得更加直观：

def fancy_dendrogram(*args, **kwargs):
	max_d = kwargs.pop('max_d', None)
	if max_d and 'color_threshold' not in kwargs:
		kwargs['color_threshold'] = max_d
	annotate_above = kwargs.pop('annotate_above', 0)

	ddata = dendrogram(*args, **kwargs)

	if not kwargs.get('no_plot', False):
		plt.title('Hierarchical Clustering Dendrogram (truncated)')
		plt.xlabel('sample index or (cluster size)')
		plt.ylabel('distance')
		for i, d, c in zip(ddata['icoord'], ddata['dcoord'], ddata['color_list']):
			x = 0.5 * sum(i[1:3])
			y = d[1]
			if y > annotate_above:
				plt.plot(x, y, 'o', c=c)
				plt.annotate("%.3g" % y, (x, y), xytext=(0, -5), textcoords='offset points', va='top', ha='center')
		if max_d:
			plt.axhline(y=max_d, c='k')
	return ddata

fancy_dendrogram(Z, truncate_mode='lastp', p=12, leaf_rotation=90., leaf_font_size=12., show_contracted=True, annotate_above=10)
plt.show()

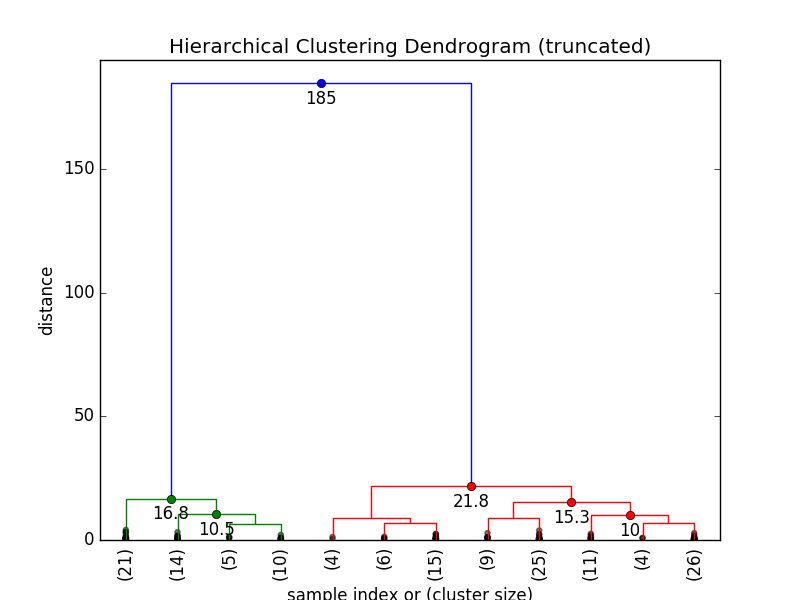
选择临界距离决定集群数量

就像我们在之前解释的那样，大距离跨度通常是我们所感兴趣的地方。在我们的例子中，我们把距离临界值设为50，因为在这里距离跨度非常明显：

max_d = 50
fancy_dendrogram(Z, truncate_mode='lastp', p=12, leaf_rotation=90., leaf_font_size=12., show_contracted=True, annotate_above=10, max_d=max_d)
plt.show()

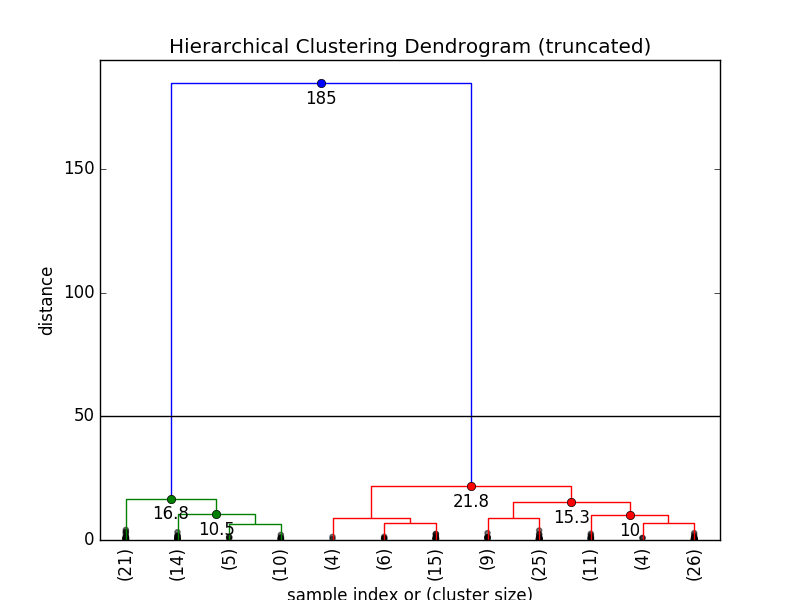
不难看出，在这一临界值内，我们有2个集群。

max_d = 16
fancy_dendrogram(Z, truncate_mode='lastp', p=12, leaf_rotation=90., leaf_font_size=12., show_contracted=True, annotate_above=10, max_d=max_d)
plt.show()

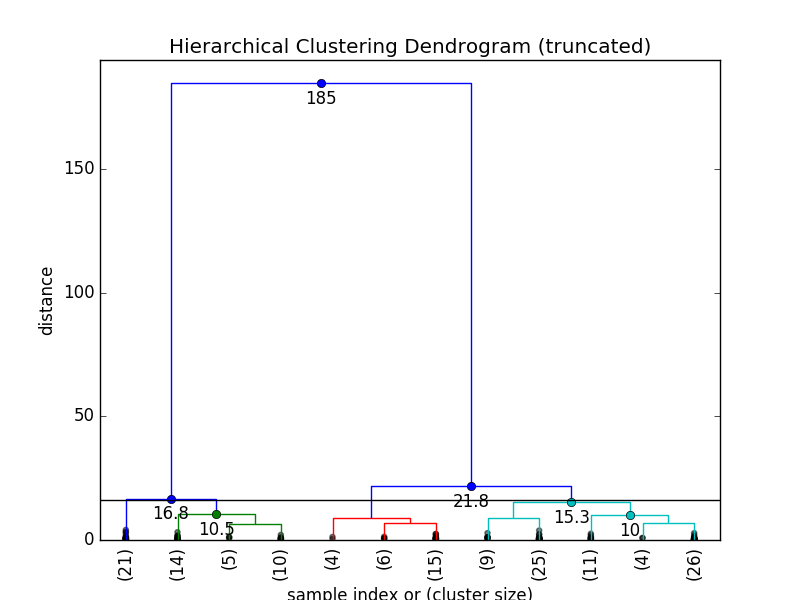
当临界值为16的时候，我们有4个集群。

获取集群信息

我们可以使用 fcluster 方程获取集群信息。

已知距离临界值

如果我们已经通过树状图知道了最大临界值，我们可以通过以下代码获得每个实验样本所对应的集群下标：


from scipy.cluster.hierarchy import fcluster
max_d = 50
clusters = fcluster(Z, max_d, criterion='distance')
print clusters

[2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1]

已知集群数量

如果我们已经知道最终会有2个集群，我们可以这样获取集群下标：

k = 2
fcluster(Z, k, criterion='maxclust')

[2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1]

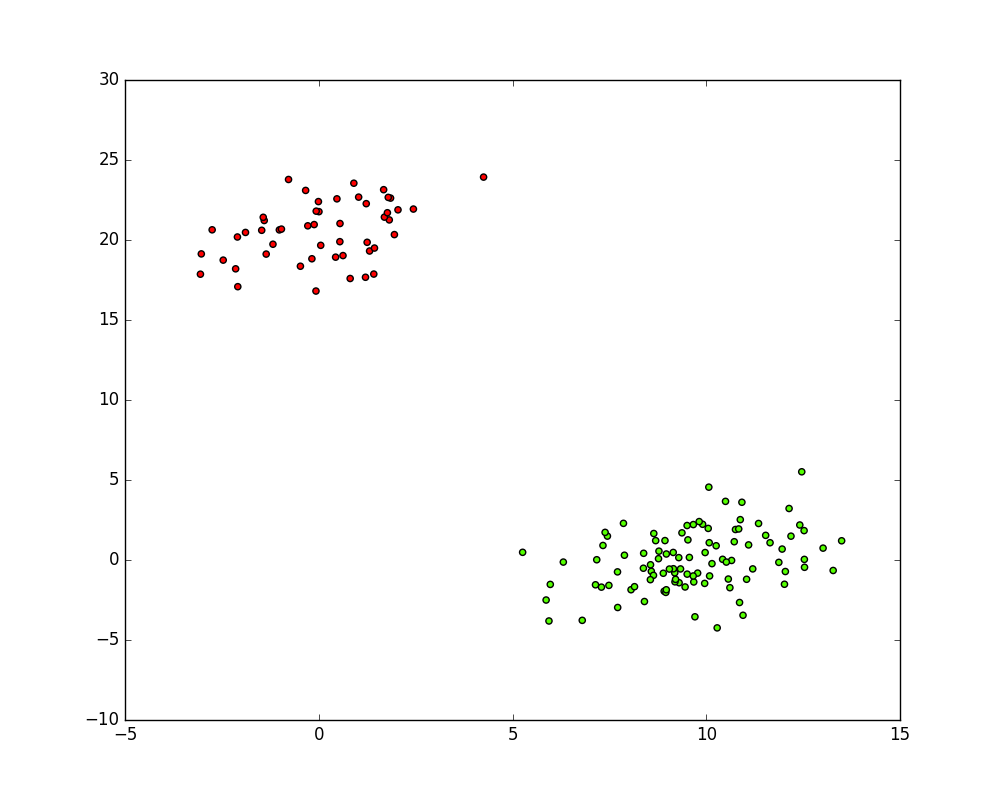
可视化集群

如果你的实验样本特征数量很少，你可以可视化你的集群结果：

plt.figure(figsize=(10, 8))
plt.scatter(X[:, 0], X[:, 1], c=clusters, cmap='prism')
plt.show()

希望本教程对你有所帮助 :smile: